TC2002极坐标测量系统在大型天线检测中的应用

  关键词：极坐标测量系统，多波束天线，坐标转换。   1. 引言用多台电子经纬仪构成的工业测量系统对大型钢结构如天线、船舶等进行安装检测的精度可达到±0.1mm左右。经纬仪工业测量系统虽然精度高，但它至少需要二台高精度的电子经纬仪及其它附件等组成系统，其成本高 ，操作人员多，尤其对测量坐标系的建立（系统定向）和维持提出了较高的要求。单台全站仪测量系统的操作方便，建立系统快，只需一台高 精度全站仪即可进行三维坐标测量，系统的成本低。如全站仪测量系统能达到亚毫米的点位测量精度，将有很好的应用前景。 LEICA公司生产的TC2002全站仪是目前全站仪中精度最高的仪器，其测角标称精度为±0.5”，测距标称精度为±（1mm+1ppm×D），但要提高坐标测量的精度，最主要的是要提高距离测量精度，而测距的固定误差和比例误差是测距误差最大的影响因 素，因此必须消除或减弱这二项误差的影响。本文提出了测出固定误差和用坐标转换求比例误差的方法大大提高了全站仪坐标测量的精度。另 外在极坐标工业测量系统中，测距的合作目标不是棱镜而是反射片，反射片的倾斜对测距精度有较大的影响，因此必须通过一定的方法，使反 射片测量的实际精度也能优于1mm，我们采用双面测距的方法有效地消除了这一误差，参文献[4]。本文最后还介绍了全站仪 测量系统在天线焦点变形检测中应用。   2. 多波束天线的模型多波束天线是某研究所的一项重要预研项目，其基本设计思 想是一个天线可安装多个馈源（波束），并且可提高天线的增益，已期达到一个天线多用的目的。预研中的小型多波束天线的面积达到6米´8米，由24块小面板拼装而成，而后续的天线面积将达到18米´24米，需要由200多块小面板拼装。在天线的安装调试过程中，传统的光学经纬仪加带尺或模板的方 法无论在精度还是速度上都是无法满足要求的，实践表明只有采用电子经纬仪交会测量系统或全站仪极坐标测量系统才能较好地解决这一问题 。     多波束天线是标准抛物线绕空间某一旋转轴旋转后所截取的一部分表面，如图1所示。我们知道标准抛物线在xoz平面坐标系中的方程为：

             &nb sp;                （1）多波束天线的旋转轴z”由z轴旋转a角，得到旋转后的z’轴，再将z’轴平移距离R得到。在x”o’z”坐标系下，多波束天线的数学方程为标准抛物线绕z”轴旋转后所得到的表面方程。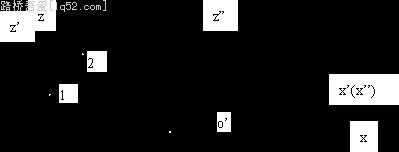              
                  o               F

图  1   将z轴旋转a角后，xoz和x’oz’坐标系的转换公式为：

             &nb sp;      （2） z’轴平移到z”的平移量为R，故有：

             &nb sp;                   （3）因此在xoz与x”o’z”坐标系的转换关系为：

             &nb sp;     （4）选取另一坐标轴y” 与x”o’z”平面垂直，且构成右手坐标系，故标准抛物线绕z”轴旋转后得到的方程为：

   （5）实际上，多波束天线是标准抛物线中的某一段（如图1中1~2弧段）绕z”轴旋转后所截取的一部分曲面。     由坐标系转换求出测量点在设计坐标系中的坐标后，即可求出该点的轴向误差和法向误差，其中 法向误差对应的就是调整量[3]。   3. 极坐标工业测量系统的应用 3.1 系统的建立极坐标工业测量系统STM的建立极为简单，只需要一台仪器即可。在工作中，我们采用TC2002全站仪、笔记本电脑、工业测量系统软件平台Axyz-CDM/STM和联机电缆等构成系统。只 需将仪器整置在附有强制对中装置的固定观测墩上，就可以进行坐标测量了。与经纬仪工业测量系统相比较，STM省略了定向过程，也就减少了由系统定向带来的误差。根据文献[4]的结论：在近距离测距 时，TC2002的乘常数可以忽略，而用交会测量结果现场修正TC2002的加常数，那么修正后的STM空间定位精度可达到±0.5mm。因此用单台全站仪测量时，须测出反射片的加常数修正值，我们在现场测量得到反射片的加常数为33.0mm(其标称值为34.4mm)。观测点的选择与天线的调整机构相联系。首先在天线面上选取十个点，这些点位分布良好，基本上能代表整个曲面，而且 每点都有已知的设计坐标。   3.2坐标系转换为了确定测量坐标系与设计坐标系间的转换参数，我们将反射片标志贴在设计点上，用全站仪极坐标测量系统测出这十个 点在测量坐标系中的坐标，然后与其设计坐标作转换，求得转换参数，如此可确定测量坐标系和天线设计坐标系（O-X²Y²Z²）之间的关系。转换参数求取后，可以将其它测量点全部转换到设计坐标系中，从而计算各个调整点的调整量，并且评定 天线的面型误差。在实际测量时，我们对多波束天线在不同状态下进行了测量和坐标转换。结果见表1、2。  

表1 天线支架水平时的坐标精度

加尺度因子改正					不加尺度因子改正
点号	DX	DY	DZ	点位精度	DX	DY	DZ	点位精度
p2	0.027	-0.443	-0.165	0.474	0.812	-0.134	-0.866	1.195
p19	-0.237	-0.201	-0.386	0.496	-1.038	0.109	-1.089	1.508
p75	-0.182	-0.104	0.095	0.230	0.124	-0.111	-0.125	0.208
p81	0.056	0.310	0.347	0.469	-0.227	0.302	0.124	0.398
p94	-0.422	0.643	-0.315	0.831	0.435	0.657	-0.344	0.860
p111	0.643	0.599	-0.315	0.934	-0.235	0.600	-0.301	0.711
p123	0.178	-0.221	0.667	0.724	0.498	-0.373	0.876	1.074
p129	-0.143	0.428	0.739	0.866	-0.434	0.272	0.948	1.077
p186	0.394	-0.296	-0.258	0.556	1.301	-0.451	0.459	1.451
p203	-0.314	-0.715	-0.408	0.881	-1.236	-0.872	0.317	1.546

表2 天线支架倾斜（工作状态）时的坐标精度

加尺度因子改正					不加尺度因子改正
点号	DX	DY	DZ	总体精度	DX	DY	DZ	总体精度
p2	-0.119	-0.063	0.769	0.781	0.601	0.221	0.127	0.653
p19	0.393	0.372	0.757	0.931	-0.340	0.655	0.114	0.747
p75	0.516	-0.334	-0.243	0.661	0.797	-0.340	-0.444	0.973
p81	-0.116	-0.243	-0.119	0.294	-0.375	-0.250	-0.323	0.554
p94	-0.127	0.116	-0.132	0.217	0.658	0.129	-0.158	0.689
p111	-0.501	-1.015	-1.087	1.570	-1.306	-1.015	-1.073	1.972
p123	-0.158	0.125	0.200	0.284	0.135	-0.014	0.392	0.415
p129	-0.852	0.404	0.356	1.008	-1.119	0.262	0.547	1.273
p186	1.040	0.079	-0.561	1.185	1.871	-0.063	0.095	1.875
p203	-0.077	0.560	0.060	0.568	-0.922	0.416	0.724	1.244

  可见，对于支架的每一种状态，坐标转换加不加尺度因子，坐标精度有较大的差异。这说明TC2002测量系统和设计坐标系间存在一个系统性的差异，经分析认为,这一差异主要是由TC2002的测距误差引起的,也即在近距离测量中,TC2002的固定误差经修正后,还有剩余误差,且剩余误差表现为系统性,只有将这个系统误差消除 才可以得到更高的转换精度，结果见下表3。表3中第三次的结果(155个点)是用二台经纬仪交会测得的结果，因此加尺度因子改正的效果不大，可见经纬仪测量系统在尺度上无大的系统误差。由于 第三次所测的点较多，有些点的调整量较大，整个面型误差也较大。另外，从表3中我们也可以知道，对于多波束这种天线来说，我们关心的是整个天线面的面型情况，而不是每个点的绝对坐标，只要天 线面上有设计坐标点，我们就可以消除全站仪坐标测量系统相对于设计坐标系的系统误差，从而使全站仪坐标测量系统的精度和经纬仪坐标测 量系统的精度能基本接近。

表 3 各种状态下的坐标转换精度

支架状态	是否加尺度改正	转换精度	尺度因子	面型误差
水    平	是	0.68	0.99975798	0.88
	否	1.09
倾斜（10个点）	是	0.86	0.99977828	0.64
	否	1.16
倾斜（155个点）	是	1.02	0.99992701	1.06
	否	1.04

  3.3 焦点位置的变形检测天线的初装是在天线面与地面近似垂直的状态下进行的，天线的焦点（相心）在测试支架上基本 处于水平状态，由于受到地面支撑，焦点的位置是保持不变的；但是天线的电信号测试是在工作状态下进行的，由于结构设计的原因导致测试 支架变形很大，从而带动焦点的位置变化，使电测无法进行下去。为此需要了解焦点的变形情况并加以修正。实测中分别检测了在测试支架处 于基本水平状态下和处于工作状态下两种情况的变形情况。  首先建立测量坐标系和设计坐标系的联系，然后采用Axyz软件中的放 样功能（BULID）将焦点的设计位置在实地标定出来。在测量过程中，焦点的附近既有副面，又有馈源，对视线有遮挡，不能直接把 焦点放样出来，因而利用馈源底部的底板，在其上布置了5个测量点（如图2所示），采用平面拟合和轴对准方法建立独立的底板坐标系，以2为坐标原点，2点到3点的连线为X轴正方向，2点到1点的方向作为Y轴正方向，按右手规则建立坐标系（图2中的Ä表示Z轴正方向指向纸里），把焦点转换到该坐标系中，可以很方便 地用卡尺放样出焦点的坐标，这一放样过程实际上也就是焦点位置的检测过程。                        
不同状态下，焦点在底板坐标系中的坐标如表4所示。  

表4 焦点在底板坐标系中的放样值

状态	X	Y	Z
1	362.219	154.111	420.179
2	357.813	155.380	422.242

   从实际测量可以看出，TC2002单台极坐标测量系统操作简单，通过测距误差改正点位精度达到亚毫米的水平，完全可以用于多 波束天线的安装调整以及类似大型工业部件的安装与检测，在大尺寸范围内可基本达到和经纬仪坐标测量系统相媲美的程度，因此为极坐标工 业测量系统在高精度的工业部件安装检测等开辟了新的领域。         参考文献： [1]李广云等，工业测量系统，解放军出版社，1994年 [2]李广云 黄桂平，最新三维工业测量系统Axyz与经纬仪模块STM/MTM，全国精密测量方法和技术在工程建设中应用学术研讨会，1998年4月，南京 [3]金超等，工业测量系统在多波束天线安装检测中的应用，解放军测绘学院学报，1998年第3期 [4]黄桂平等，TC2002极坐标测量系统的实际精度分析， ’98中国测绘学会测量仪器专业委员会综合学术年会，1998年10月，郑州